乐音的音色
我们听到的乐音都是有一个能量最高的基频和一系列泛音组成的,这在前文已经解释过了。人耳对4000Hz左右的声音最敏感,绝大多数乐音的泛音列正处在这个频段,因此,泛音的成分决定了音色的不同。
同一音高的乐音,在不同乐器上的音色不同,这是因为发声构造的差异导致的泛音比例差异。同一乐器的音色特征明显,可认为泛音比例是固定的。不同音高彼此之间的和谐程度是不同的,其中要以基频相差2倍的音组成的和声(Harmony)最为和谐。
我们首先尝试合成乐音。假设乐音主要由基音$f_0$和若干泛音$f_1, f_2, \dots, f_n$合成,其振幅用一个正项数列${a_n}$ 表示。实验2.1尝试合成多种乐音,其中2.1.1&2.1.2 用$a_n=n^{-2}$和$a_n=n\exp(-n)$两个衰减的数列合成了乐音,2.1.3根据钢琴的音频逆向合成了钢琴的声音。
和声的和谐程度
同时发出不同频率的声音,有的和谐,有的冲突。本节尝试从不同角度解释这种现象。
纯音
从微观角度看,不同的频率的若要同步,则需分别经历若干个周期后,其相位差出现公共周期变化。这种公共周期越短,其规律越容易被人耳捕捉到,听起来越和谐。连续变化的频率比,理论上不存在整数比。但由于人耳的灵敏度是有限的,会用近似的整数比得到公共周期。如果整数过大,周期会变大,规律不明显,这时的和声就很不和谐。
连分数(continued fraction)可以近似地表示小数。要计算实数 $x$ 的连分数表示,写下 $x$ 的整数部分。从 $x$ 减去这个整数部分。如果差为 0 则停止;否则找到这个差的倒数并重复。这个过程将终止,当且仅当 $x$ 是有理数。例如,数 $3.14159$,可以用连分数展开 $[3;7,15,1,25,1,7,4]$表示。显然对于任一实数,也可以用无限长的连分数近似地逼近。
| 连分数 | 最简分数 | 绝对误差 |
|---|---|---|
| $[3;7]$ | $22/7$ | $1.267143\times 10^{-3}$ |
| $[3;7,15]$ | $333/106$ | $-8.056604\times 10^{-5}$ |
| $[3;7,15,1]$ | $355/113$ | $2.920354\times 10^{-6}$ |
| $[3;7,15,1,25]$ | $9208/2931$ | $-9.894234\times 10^{-8}$ |
| $[3;7,15,1,25,1]$ | $9563/3044$ | $1.314060\times 10^{-8}$ |
| $[3;7,15,1,25,1,7]$ | $76149/24239$ | $-4.125580\times 10^{-10}$ |
| $[3;7,15,1,25,1,7,4]$ | $314159/100000$ | No error |
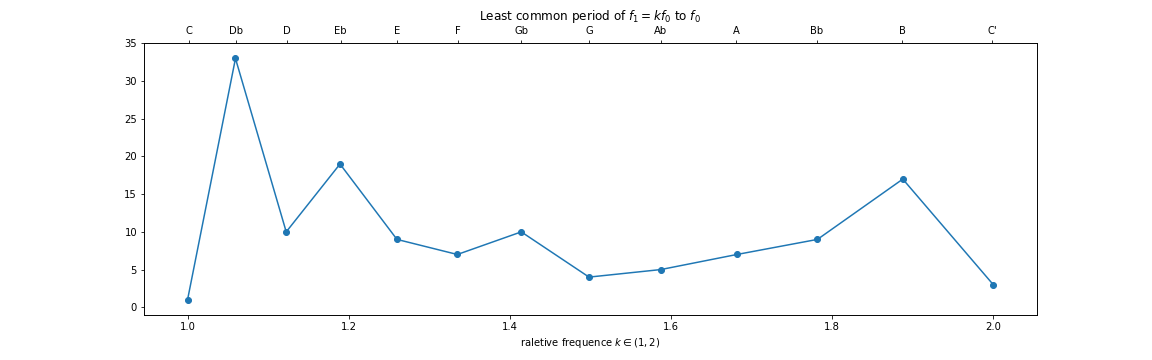
实验2.2.1计算频率为$f_0$和$f_1\in(f_0,2f_0)$的最小公共周期,计算中至多取三项连分数表示。
由于频率相差很小时,即可认为和声的公共周期为1,也可认为公共周期很大,为了消除这种矛盾,我们认为一个频率窗口内$(f-r,f+r)$内的音都是同一个音,公共周期取这个区间内最小的公共周期。由此,可以粗略地度量十二平均律的基本音级之间的和谐程度,结果如下。
乐音
乐音由一系列的泛音构成,本节尝试借助KL散度的定义,从宏观角度量化两个乐音之间的距离,两个乐音之间的距离越小,则听起来越和谐。
假设频率为$f$的乐音,频谱为$F(\omega;f)$, ${a_n}$ 是一个趋于零的有界正项数列,用于表示基音和泛音列的能量强度。 $\delta$可视为一个冲激函数, 用方差很小的高斯函数代替。则有
频谱$F(\omega;f)$ 经过归一化, 满足 $|\int_{-\infty}^{\infty}F(\omega;f)\mathrm{d}\omega|=\sum |a_k|=1$
令$f_1<f_2$,则频率分别为$f_1,f_2$的两个乐音$p_1,p_2$之间的距离为
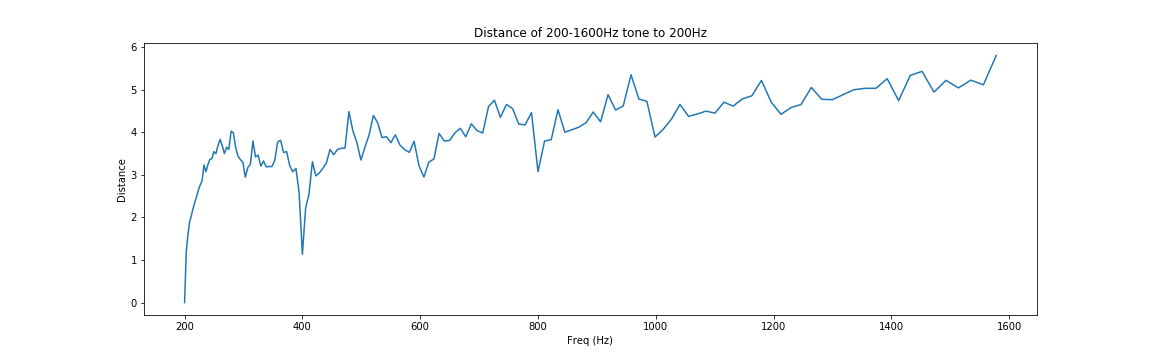
\[D_{\text{KL}}(p_2 \| p_1) = \int_{\infty}^{\infty}|F(\omega;f_1)|\ln\left(\left|\frac{F(\omega;f_1)}{F(\omega;f_2)}\right|\right)\mathrm{d}\omega\]实验2.2固定了$f_1$作为标准音的频率,选择不同的$f_2$作为基频合成了测试音,验证了如果 $f_2 - f_1 > \epsilon >0$ ,那么当$f_2=2f_1$时, $D_{\text{KL}}(p_2 \| p_1)$ 最小。
实验2.3在图表上直观地呈现了在一倍频率内$[f_0,2f_0]$,合成乐音到最低音$f_0$之间的距离。
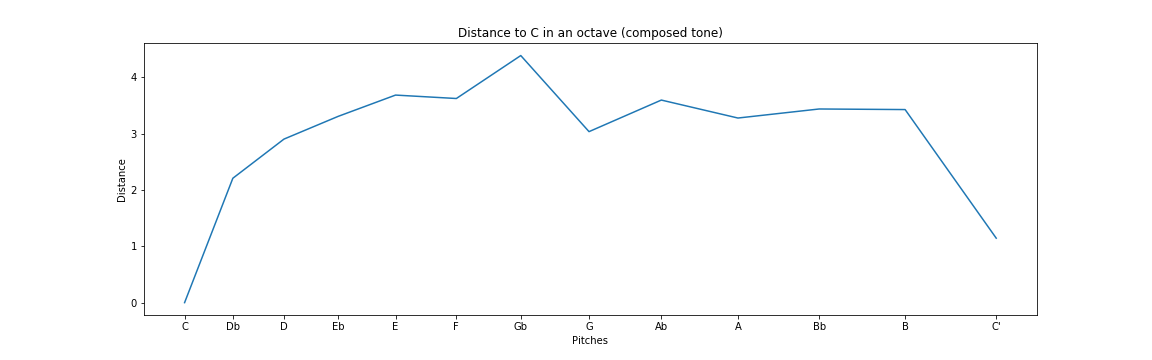
运用同样的方法,展示了合成音和钢琴音在小字一组c1到小字二组c2范围内关于c1的距离。