音律——为什么是do,re,mi,fa,sol,la,si?
音律(Musical temperament) 是制定音高的标准,只有音高确定了,才能准确地记录旋律。为了方便理解,我们先从 十二平均律(Twelve-tone equal temperament,12 equal temperament, 12-TET or 12-ET) 讲起。
十二平均律
我们知道频率相差一倍的音听起来最和谐,可以把它们当做同一种音。十二平均律把2倍平均分成12个均等的部分—— 半音(Semitone) ,确定了12种不同的音高,以此来组成旋律。显然,平均分成12份是等比分割的,否则再经过12个半音,频率不能翻倍。相邻两个半音的频率之比为$2^{1/12}$, 全音(Whole tone) 间的音高距离等于两个半音。当一个音高的频率确定后,其他所有的音的频率也能随之确定。平均律因为转调方便,适合协调多种乐器,已经成为了现代音乐的标准。
C,D,E,F,G,A,B作为七个基本音级(Step)的音名,在乐音体系中循环使用,do,re,mi,fa,sol,la,si是其对应的唱名。除了B、C,E、F之间是半音关系外,其他连续基本音之间都相差了一个全音。由于其余5个半音没有独立的名称,需要借助 变音记号 来表示,升记号 ♯(Sharp) 把基本音升高一个半音, 降记号♭(Flat) 把基本音降低一个半音, 重升记号 𝄪 (Double sharp) 把基本音升高一个全音, 重降记号𝄫 (Double flat) 把基本音降低一个全音,还原记号 ♮ (Natural) 表示将已经升高或降低的音还原。在钢琴中,这七个基本音级在白键,其余五个半音在黑键。音级之间的距离成为 度(degree),下图C-B为一个七度。

国际标准规定A4 = 440 Hz,下表列出了乐音体系中,部分音名跟频率的关系。
| 音名 | 频率(Hz) | 音名 | 频率(Hz) | 音名 | 频率(Hz) |
|---|---|---|---|---|---|
| $\text{C}3$ | 130.81 | $\text{C}4$ | 261.63 | $\text{C}5$ | 523.25 |
| $\text{C}^{♯}3,{\text{D}}^{♭}3$ | 138.59 | $\text{C}^{♯}4,\text{D}^{♭}4$ | 277.18 | $\text{C}^{♯}5,\text{D}^{♭}5$ | 554.37 |
| $\text{D}3$ | 146.83 | $\text{D}4$ | 293.66 | $\text{D}5$ | 587.33 |
| $\text{D}^{♯}3,\text{E}^{♭}3$ | 155.56 | ${\text{D}}^{♯}4,\text{E}^{♭}4$ | 311.13 | $\text{D}^{♯}5,\text{E}^{♭}5$ | 622.25 |
| $\text{E}3$ | 164.81 | $\text{E}4$ | 329.63 | $\text{E}5$ | 659.26 |
| $\text{F}3$ | 174.61 | $\text{F}4$ | 349.23 | $\text{F}5$ | 698.46 |
| $\text{F}^{♯}3,\text{G}^{♯}3$ | 185.00 | $\text{F}^{♯}4,\text{G}^{♭}4$ | 369.99 | $\text{F}^{♯}5,\text{G}^{♭}5$ | 739.99 |
| $\text{G}3$ | 196.00 | $\text{G}4$ | 392.00 | $\text{G}5$ | 783.99 |
| $\text{G}^{♯}3,\text{A}^{♭}3$ | 207.65 | $\text{G}^{♯}4,\text{A}^{♭}4$ | 415.30 | $\text{G}^{♯}5,\text{A}^{♭}5$ | 830.61 |
| $\text{A}3$ | 220.00 | $\bf{A4}$ | 440.00 | $\text{A}5$ | 880.00 |
| $\text{A}^{♯}3,\text{B}^{♭}3$ | 233.08 | $\text{A}^{♯}4,\text{B}^{♭}4$ | 466.16 | $\text{A}^{♯}5,\text{B}^{♭}5$ | 932.33 |
| $\text{B}3$ | 246.94 | $\text{B}4$ | 493.88 | $\text{B}5$ | 987.77 |
下图是标准钢琴的键盘,有88个音高不同的键,是音域最广的乐器之一,覆盖了A0-C8,青色标注的键是中央C,黄色标注的键是标准音A(440Hz)。除此之外的音,因为太低或太高,人耳无法很好地分辨音高,在音乐中几乎是不用的。
三分损益律(五度相生律)
三分损益律是比十二平均律历史更悠久的音律,影响了十二平均律和七个基本音级的成型。
我们知道乐音的是由基音和泛音组成的。基音和第一泛音之间形成 八度(octave) 关系,是除基音本身之外和基音最和谐的一个泛音,它控制了基本音级之间的循环。为了确定出八度之间的其他音高,可以用第二泛音生律。
考虑一段均匀的空气管(琴弦音高还受张力影响,因此不用琴弦),它发声的频率为$f$,把这个音作为起始音$P_0$。 第二泛音$3f$是三次谐波,把三次谐波降低一个八度,就得到了一个八度以内对应的音$P_1$,它的频率是$1.5f$,对应空气管的长度变成原来的$2/3$,减少$1/3$。重复这个操作可以下一个音$P_2$,注意到$1.5\times 1.5>2$,因此需要再除以2,$P_2$的频率是$P_1$的$3/4$,对应空气管的长度变成上一步的$4/3$,增加$1/3$。这种生律方法称为三分损益法,三分损益律因此得名。由于它生成音级的顺序是五度关系,因此又叫 五度相生律。
下面演示如何从起始音得到一个八度内的十二个半音,这里令 1 = C = 宫。
| 音高排序 | 简谱符号 | 西方音名 | 五声音名 | 相对频率 | 平均律相对频率 |
|---|---|---|---|---|---|
| 0 | 1 | C | 宫 | $2^0 3^0=1.000000$ | $2^{0/12}=1.000000$ |
| 7 | 5 | G | 徵 | $2^{-1}3^1=1.500000$ | $2^{7/12}=1.498307$ |
| 2 | 2 | D | 商 | $2^{-3}3^2=1.125000$ | $2^{2/12}=1.122462$ |
| 9 | 6 | A | 羽 | $2^{-4}3^3=1.687500$ | $2^{9/12}=1.681793$ |
| 4 | 3 | E | 角 | $2^{-6}3^4=1.265625$ | $2^{4/12}=1.259921$ |
| 11 | 7 | B | 变宫 | $2^{-7}3^5=1.898438$ | $2^{11/12}=1.887749$ |
| 6 | ♯4 | G♭ | 变徵 | $2^{-9}3^6=1.423828$ | $2^{6/12}=1.414214$ |
| 1 | ♯1 | D♭ | 变商 | $2^{-11}3^7=1.067871$ | $2^{1/12}=1.059463$ |
| 8 | ♯5 | A♭ | 变羽 | $2^{-12}3^8=1.601807$ | $2^{8/12}=1.587401$ |
| 3 | ♯2 | E♭ | 变角 | $2^{-14}3^9=1.201355$ | $2^{3/12}=1.189207$ |
| 10 | ♯6 | B♭ | 闰宫(清羽) | $2^{-15}3^{10}=1.802032$ | $2^{10/12}=1.781797$ |
| 5 | 4 | F | 清角 | $2^{2}3^{-1}=1.333333$ | $2^{5/12}=1.334840$ |
| $2^{-17}3^{11}=1.351524$ | |||||
| 0 | 1 | C | 宫 | $2^{-19}3^{12}=1.013643$ | $2^{0/12}=1.000000$ |
注意到$\log_2 3\approx19/12$,经过12次生律之后,得到了和初始频率很接近的音,可认为没有产生新的音级,回到了初始音级。下面分析三分损益法在音高上的均匀性。
如果运用k次三分损益法,生成了包括 $k+1$ 个不同的音级 $\{P_0,P_1,\dots,P_k\}$ ,把他们的相对频率 $\{1,f_1,f_2,\dots,f_k,2\}$ 升序排列,得到数列 \(\{a_n\}_{n=0}^{k+1}\) 。 取对数并差分 $b_i = \log a_{i+1}- \log a_i$,得到\(\{b_n\}_{n=0}^k\) 。
下图展示了 \(\{\log a_n\}_{n=0}^{12}\) 的分布情况,可认为 \(\{a_n\}_{n=0}^{12}\) 近似是一个等比数列。
\(\{ b_k\}\) 的标准差 $s$ 刻画了\(\{ a_k\}\)整体不均匀的程度。\(\max\{ b_k\}/\min\{ b_k\}\) 则表示\(\{ a_k\}\)偏差的上限,这个上限越接近1,则越均匀。将两者相乘,作为衡量\(\{ a_k\}\)是否分布均匀的指标,可以看到当 $k=4,6,11$时,有三个极小值点,此时分音是相对均匀的,这也是五声音阶,七声音阶,半音阶的由来。关于音阶,会在后面的文章详细介绍。
观察钢琴键盘,可以发现五声音阶(黑键)和七声音阶(白键)关于半音阶是互补的。
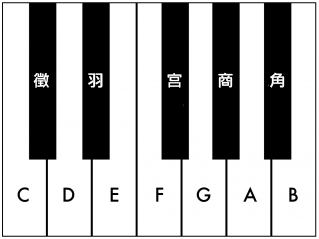
纯律
观察C4的泛音列
| 基音(f) | 第一泛音(2f) | 第二泛音(3f) | 第三泛音(4f) | 第四泛音(5f) |
|---|---|---|---|---|
| C4 | C5 | G5 | C6 | E6 |
五度相生律用第二泛音作为生律要素,用到了质数3;而纯律还用第四泛音作为生律要素,用到了质数5。
纯律希望用尽可能简单的整数比来确定音高。首先从利用三次五度相生律,得到五度排列的四个音,F——C——G——D,再依次寻找F,C,G的第四泛音A,E,B,构成七个基本音级,组成旋律。这样,F-A-C,C-E-G, G-B-D,分别构成一个三和弦。关于和弦的内容,也会在后面的文章详细介绍。
| 音名 | 相对频率 | 平均律相对频率 |
|---|---|---|
| C | 1.000000 | 1.000000 |
| D | 9/8=1.125000 | 1.122462 |
| E | 5/4=1.250000 | 1.259921 |
| F | 4/3=1.333333 | 1.334840 |
| G | 3/2=1.500000 | 1.498307 |
| A | 5/3=1.666667 | 1.681793 |
| B | 15/8=1.875000 | 1.887749 |


